For those of you unfamiliar with it, here's a brief example. Let's say you're the Blue Yuppies, a political party that is really popular with the hipster downtown folk, but not so much with suburban soccer moms. You won the last election in a city with four seats, but have lost popularity recently, and your polling tells you that neighborhoods in your city would vote like this in an upcoming election:
 |
| Super idealized city |
 |
This is what gerrymandering is. Redistricting is a huge power to have over your opponents between elections, because it can be leveraged quite well to retain power even against the popular vote of an area. And it's not always necessarily about giving yourself the comfortable easy seats - as in the bottom right example above, lumping all your opponent's support together can be a very effective way to secure the rest for yourself.
This often results in very funny looking districts. In the first three examples above, you could maybe justify most of the districts as effectively representing a region of the city. The gerrymandered one, though, has long snaky districts, in order to get the right sorts of people voting together.
Gerrymandering is alleged to happen in the USA a lot. Take a look at some of these examples and decide for yourself:
 |
| Capture ALL the cities! |
 |
| Snaky... |
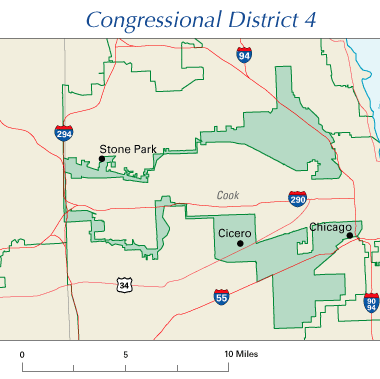 |
| Because you know that highway is an important part of the district... |
After too many shenanigans like this going on, some states are starting to insist on bipartisan committees to come up with new district boundaries, hoping to take the advantage away from the parties in power. The problem with this, though, is that the only thing the committee members from different parties tend to agree on is that they don't want to lose the next elections, and they may end up carving out districts that serve mostly to maintain their seats, leading to safe and boring elections. Yikes.
Canada, on the other hand, tends to have completely independent commissions in charge of redistricting, with the goal of avoiding gerrymandering. But how well does our system actually work?
One way to check for potential gerrymandering is to check a district for its compactness. The underlying assumption here is that no point in a riding should be too far away from the middle, and that the riding should represent a reasonably consistent geographical area. Shapes like circles or squares are the most compact, shapes like Congressional District 4 up there aren't.
This fun report took a very in-depth look at compactness in voting districts in both the US and Canada. They measured compactness by comparing the perimeter of a district with the square root of the area, and then factored it so that a perfect square has a compactness value of exactly 1.
So how did Canada compare to the US? The average compactness values for 2006 were:
- Canada: 1.400
- USA: 2.103
From the report, the historical comparisons look like this:
 |
| Hill, 2009 |
For reference, if the average national districts were rectangles with the same areas, this is how they'd look:
So on that measure, Canada's pretty much always been better than the USA in terms of compactness (and, implied, in terms of likely gerrymandering), and the USA has seen a marked increase since about the early 1990s.
But wait! Canada just did a full round of redistricting! We now have 338 ridings instead of 308. These are exciting times! Just how well did the commission do?
My analysis of the 338 districts using the same methodology as Hill (2009) shows an average compactness of: 1.408. In other words, nothing too much to worry about form a gerrymandering point of view! Hooray Canada for mostly transparent electoral systems!
The averages per province ranged from 1.27 for PEI to 1.59 for New Brunswick, and only six federal ridings had a compactness score worse than the average American district.
 |
| Saskatchewan was solid (average: 1.31) |
 |
| Newfoundland and Labrador averaged 1.52, because shores are tricky |
The great thing is that Canadian boundaries are still good, even at the provincial legislature level. Of Alberta's 87 provincial electoral districts, the average compactness is still only 1.440, very similar to the federal average and still way lower than the American average. In fact, only one Albertan district is worse than the average American district. Take a look at this super cool interactive thingy I made:
With the exception of Chestermere-Rocky View (which looks like it's giving Calgary a hug), all of these ridings are pretty reasonable, and they're all better than the average American voting district.
Go Canada! Our politics may not always be pretty, but at least there's no sign of anyone actively tinkering with them!
Go Canada! Our politics may not always be pretty, but at least there's no sign of anyone actively tinkering with them!

11 comments:
Compactness is definitely desirable for any voting district but keep in mind that compact configurations can still be used to dilute certain voting demographics and favour certain parties. The case has been seen in many 'rurban' districts in Saskatchewan and Alberta prior to this year's reconfiguration. Some have protested the new alignments claiming that it would initiate an urban and rural divide.
That said, wouldn't it be interesting to see proportional representation occur in our lifetime?
I'd be interested to see that Alberta map superimposed with a poll of where people usually vote, because the conservative party has been accused of gerrymandering. I agree with Paul, I'd much rather see proportional representation than keep status quo with our electoral system.
The 'compactness' will surely be related to the local population density, as size of the voting districts will be inversely proportional with this metric, and necessity of making very sharp cuts through the geography will be diminished. As the population density of the US (even including Alaska) is nearly an order of magnitude higher than that of Canada, it should be expected that the 'compactness' will be higher in the US. I'd imagine that if the 'compactness' to population density of all of the voting districts were plotted, you'd see a strong correlation - something to look into.
Additionally, the term 'compactness' is a poor choice, since larger 'compactness' means it is in fact less compact, so the term should by diffuseness or something similar.
The choice of definition of the metric used is also poor, as something that is very compact, but has surface roughness could rate as high as a region which is actually what you want to define as not ideal. Indeed, you concede that regions like Labrador, which are along coastline, will surely have a large perimeter length even though they are close to being as compact as it can be. A better way would be to divide the area of the voting district by the area of the convex hull. In this case, a compactness of 1 still signifies the ideal square situation (and indeed any convex shape like a circle or rectangle), and lower values are less ideal. The area of the convex hull can also be altered to discount any regions cutting over water, eliminating the issue of coastline. If you wanted to penalize elongated but convex districts, you incorporate the aspect ratio of the convex hull as an additional factor, but I find the thing that people recognize most abhorrent about gerrymandering is the exaggerated concavity of polygons used to bound districts.
Now, you may still find that Canadians are more honest and less prone to gerrymandering than Americans, but I feel like this alternate method would show this with more confidence.
Very interesting article, however your data is off by a few years. California was redistricted in 2012 using a bipartisan commission with data from the 2010 census. This resulted in more competitive districts and a top-two blanket primary. The districts you showed are prime examples of how gerrymandering was out of control in the state. If you look at the districts now, you can see more cohesive, contiguous areas.
I think two things could be done to improve this analysis. First would be to give ridings that run along physical/provincial boundaries a lower weighting (could part of the difference between Canada and the US be that Canada has more regularly shaped provinces?). Second, a comparison to population density per riding. Ideally, a riding would not be 90% rural and 10% urban (like the two for Alberta that split up Fort MacMurray).
great post and good thinking about gerrymandering..go ahead I am agree with your opinion. thanks for sharing this with us.
Hello dear admin
How are you? with their new wash/dry/fold service, all you need to do is drop in your clothes and collect them later on after they have been washed, dried and folded - within 24 hours.Read more at-:Toronto coin laundry
I am so happy today and appreciate the genuine work done by the love spell caster and give me the right direction so today I got my wish fulfilled under the guidance of a love caster Dr Jumba . Love is an important part of our relationship. I can understand this when my boyfriend has cheated on me and engaged with other girl’s affairs. At that time I was Broken and realized the importance of love in my life or relationship. My boyfriend did not give me importance and he always embarrasses me in front of his friends. Then I searched on the Internet and I found a spell caster who i trusted and he cheated me “one day a friend of mine told me about a real spell caster who helped her with a love spell so I got the contact number of Dr Jumba spell caster ” then I dropped a message on WhatsApp and explained all my problems to him . So he showed me previous work done by himself and guided me on how the work will be done. Then I start work and get my boyfriend back within 24 hours as Dr Jumba promised me in a positive way. I want to use this time to show appreciation. That's why I am so happy and thankful to Dr Jumba. he can also help you below are his contact information email : wiccalovespelltools@yahoo.com text or call him +19085174108 .
website :https://drjumbaspellhome.wordpress.com
Omg I Finally Got Helped !! I'm so excited right now, I just have to share my testimony on this Forum.. The feeling of being loved takes away so much burden from our shoulders. I had all this but I made a big mistake when I cheated on my wife with another woman and my wife left me for over 4 months after she found out.. I was lonely, sad and devastated. Luckily I was directed to a very powerful spell caster Dr Emu who helped me cast a spell of reconciliation on our Relationship and he brought back my wife and now she loves me far more than ever.. I'm so happy with life now. Thank you so much Dr Emu, kindly Contact Dr Emu Today and get any kind of help you want.. Via Email emutemple@gmail.com or Call/WhatsApp cell number +2347012841542 Website (https://emutemple.wordpress.com/)
Omg I Finally Got Helped !! I'm so excited right now, I just have to share my testimony on this Forum.. The feeling of being loved takes away so much burden from our shoulders. I had all this but I made a big mistake when I cheated on my wife with another woman and my wife left me for over 4 months after she found out.. I was lonely, sad and devastated. Luckily I was directed to a very powerful spell caster Dr Emu who helped me cast a spell of reconciliation on our Relationship and he brought back my wife and now she loves me far more than ever.. I'm so happy with life now. Thank you so much Dr Emu, kindly Contact Dr Emu Today and get any kind of help you want.. Via Email emutemple@gmail.com or Call/WhatsApp cell number +2347012841542 Website (https://emutemple.wordpress.com/)
Are you having issues in your relationship, Or finding it difficult to have a child of your own or are you the type having any diseases in your body. I will advise you to contact Dr. Perfect of ( Perfectlovetemple@gmail.com ).The potency of his spell is so effective and can reunite broken relationships and can also make one get pregnant no matter the situation and not only that, He also has the power to cure all types of diseases within the period of 48hours.Contact him today and thank me later. Contact details :;( Perfectlovetemple@gmail.com ) //
Post a Comment