It seems like with increasing frequency we hear about rising inequality, both with wealth and income distribution across our country and the world as a whole. We see articles regularly like this and this, accurately describing it as a major issue for our times.
With so much interest in the topic, it’s probably unsurprising that it’s a well-studied field. Before you can properly wrap your head around something you have to measure it, and in order to get policy makers to pay attention you pretty much have to boil that measurement down to a single number. So it isn’t shocking at all that economic inequality can be measured by a single value, known as the Gini Coefficient.
I Dream of Gini
To start looking at measuring inequality we can survey a population, rank people based on their wealth, and compare the percentage of people poorer than a given person to the percentage of wealth held by people poorer than that person. Effectively, these two values will be identical in a purely even distribution but further apart as the inequality starts to grow. If everyone has the same wealth, then the poorest 20% of the population will have 20% of the money, and the poorest 70% will have 70% of the money. If we plot this, we’d get a straight line of equality:
A more unequal distribution might look like this, though, where the poorest 20% only has 5% of the wealth, and the poorest 70% only has 50%:
The Gini coefficient compares these two curves, the equality curve and the actual curve of the population, by comparing the area under the actual curve (B) to the area between the curve and the line of equality (A). The bigger the area between the curves (Area A), the bigger the Gini coefficient, so a Gini of 0 means a perfectly equal society, and a Gini of 1 means effectively that all the wealth is concentrated in the hands of one person.
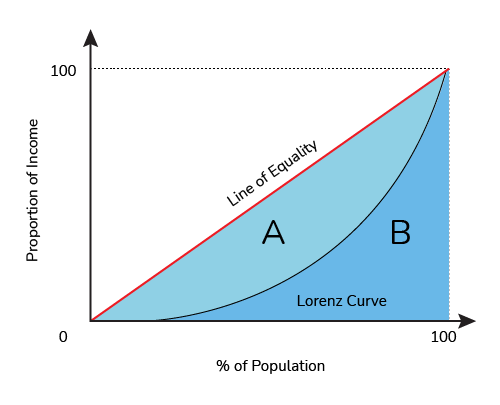
Gini in a Bottle
The Gini coefficient isn’t a perfect way of measuring inequality, but does a pretty good job. In the absence of social programs like a universal basic income, it’s worth pointing out that there will probably always be a non-zero Gini income coefficient, and that that’s not inherently evil. For instance, people late in their careers tend to make more money than newborn infants, and we’re generally ok with that.
The Gini coefficient also could give the same number to different distributions, if the shape of the curve is different but still results in the same relative areas. This means that overall it’s better as a relative indicator of inequality than a pure comment on the status of a society.
Unleash the Gini
As a very basic example for figuring out a Gini coefficient of our very own, we can take a look at a 10 player “Sit n Go” poker tournament. Following a common model used in online tournaments, 10 players sign up and the winner gets 50% of the pot, second place gets 30%, and third place gets 20%. Everyone else gets nothing, though hopefully has lots of fun too.
If we wanted to plot the curve we talked about before (incidentally, called a "Lorenz Curve"), we could use the information that the bottom 70% (the 7 losers) get 0% of the wealth, the bottom 80% (7 losers + third place) own 20% of the wealth, and the bottom 90% own 50%. Put that all together and we get this graph:
 |
Area A, between the curves, can now be compared to the total area of A+B, and we get a Gini coefficient of 0.76.
Before we get to the actual point of all this, it’s worth taking a second to reflect here. Splitting a population into ten groups and having 50% of the wealth go to the group that's best at poker is no basis for a system of distributing wealth. That's 50% of all cash, stocks, bonds, houses, privately held land, and super yachts. Extending the analogy, even if we were to pretend that the "best" 10% is who ends up with half the wealth, where here poker ability might correspond to concepts like hard work, diligence, education, etc, that still feels raucously unfair to end up with a distribution as shown above. And that's ignoring the fact that a significant proportion of wealth is significantly correlated to the wealth of one's parents, negating a lot of the 'hard work' argument.
So here's the issue. The Gini coefficient for the distribution of wealth in a 10 player online poker tournament is 0.76. The Gini coefficient for the distribution of wealth in Canada is 0.73.
Now on the one hand, admittedly there's a little bit of room between 0.73 and 0.76. 0.76 is about the same relative inequality as in Vietnam, a bit worse than a country like Egypt (0.756) and a bit better than a country like Bolivia (0.764).
On the other hand, Canada is about the same as countries like Uganda and Liberia, which may come as a surprise to some overly self-righteous Canadians. As well, the most recent statistics are from 2019, and studies show that inequality has only risen during the Covid-19 pandemic.We very well could be worse off than if our society had been set up as though by poker tournament.
Another thing to mention is that, as I said before, the Gini coefficient doesn't really comment on the shape of the Lorenz curve, just the area. And obviously Canada doesn't have 70% of people with absolutely no wealth, so maybe while the numbers are similar they don't mean the same thing, maybe it isn't quite as dire as it sounds?
Unfortunately it's not that simple. A 2012 report from the Broadbent Institute showed this graph for Canada:
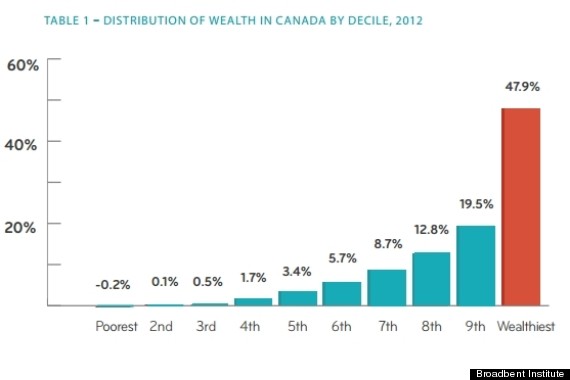
Shockingly, the top 10% (at that time) ended up with almost half the wealth, not far off from the poker example. The bottom 10% didn't just have “no wealth”, they owed more than they owned. I'd argue that if you want to think about just how rich the rich are in Canada, a 10 person poker tournament is, distressingly, actually a very good analogy.
As an aside, at least in terms of poker analogies, things can always get worse. The $10,000 Main Event at the World Series of Poker handily posts its payout table online, and if you do a similar analysis you get something much much worse:
This Gini coefficient comes in at a whopping 0.94, thankfully much higher than any real country. This is what a Lorenz curve looks like when 0.5% of the population has 50% of the wealth, and is genuinely terrifying to contemplate as a future if we don't sort things out in the real world.
Canada has a long way to go in terms of wealth inequality, but obviously it gets worse too. The United States (0.852) and Russia (0.879) have absurdly high wealth inequalities. But worst of all? The world as a whole, sitting at a Gini coefficient for wealth distribution of 0.885. We have the means to measure this and the tools to do address it, and it's well past time we do something about it.



7 comments:
The cornerstone of coursework writing help is its team of expert writers. These individuals are well-versed in various subjects, ensuring that each assignment is approached with precision and expertise.
BECOME A MULTI MILLIONAIRES WITH GLOBAL INFLUENCE, THE GREAT ILLUMINATI CAN MAKE EVERYTHING POSSIBLE, VIA.... {{ILLUMINATI SECRETE TEMPLE666@YAHOO.COM}},...........
🚨🚨 YOU EVER GOT SCAMMED, THEN YOU SHOULD READ THIS 🚨🚨🚨
You could probably get your money back, and I said probably, This is because most scammers don't move the money to a bank account, most scammers move it to a crypto currency wallet or a local money saving platforms, this way they stay undetected and noticed by authorities.
What you have to keep in mind is, this crypto wallet can be reported or hacked into, and this is what we do.
WHO ARE WE⁉️ YOU MIGHT ASK❗❕❗❕
We are ⭐PYTHONAX⭐ a group of skilled and experienced internet and computer experts. We have refocused our work force into tracking down scammers and helping victims of scam recover their money, or what's left of it. Using our experience in transactions tracking and jail breaking, we can now guarantee scam victims an opportunity to recover their money.
There are so many ways to get scammed in the world we live in today, majority of this scams are internet based scam, one of the major disadvantages of the internet. Here are examples of scams we have dealt with and can help such victims to this scams as well-:
❌Cryptocurrency investments scammed victims.
❌Forex/Binary Option investments scam victims.
❌Buying and Selling scam victims.
❌Dating & Romance scam victims.
❌Loans scams victims.
❌Housing & Estate Investments Scam victims. E.t.c.
How services are simple and and a breakdown of each steps of the process we will take to help you get your money back would be explained and told to you, what we do isn't illegal, we try and follow the rules and make sure you aren't involved in any crime. You can choose to remain anonymous, your personal info wouldn't be required of you, all we need are infos regarding the scam, infos like-:
1️⃣ Total Amount of what you were scammed.
2️⃣ The type of scam you were involved in.
3️⃣ The means of Communication you used in communicating with the scammers. Eg, emails, numbers or social media handles......
4️⃣ Details of which you used to make payments and transactions ID.
Do not feel shy or ashamed or stupid, this scammers are really good at what they do, they make everything look so real and convince and very very real like the actual real stuff.
Use this emails below to contact us-:
PYTHONAXHELP@PROTONMAIL.COM
PYTHONAXSERVICES@PROTONMAIL.COM
We assure you of no form of judgements or guilt, we are professionals and only want to help
This is a very good post with solid information, but your post is very not so good in engaging readers visually. Adding graphics or charts could take this post from good to excellent.
auto insurance
Looking to Buy Google Reviews? Our service offers genuine, high-quality reviews to boost your business reputation. Increase visibility, attract more customers, and enhance your online presence. Fast delivery, 100% authenticity, and excellent customer support. Get started today!
Boost Your Business with Our Trusted Google Review Services:
✔ 100% Customer Satisfaction Guarantee
✔ Genuine, Safe Google Reviews
✔ Male and Female Profiles Available
✔ 100% Non-Dropped, Permanent Reviews
✔ Real User, Active Google Accounts
✔ Reviews from the USA, UK, Canada, Australia, and 100+ Countries
✔ Affordable Pricing for Every Budget
✔ Money-Back Guarantee
✔ Super Fast Delivery
Read More: Buy Google 5 Star Reviews
Buy Yelp Reviews - CreativeSmmIT
This is my testimony about how I finally joined the New World Order, the Illuminati, after over two years of trying to join, but scammers kept taking my money. I wanted to join the Illuminati for so long, but scammers kept taking my money until earlier this year, when I met Lord Felix Morgan online. I contacted him and explained everything. He recommended I register, and I paid the large membership fee to get started. I was inducted into the World Order and received the sum of $1,000,000 upon induction. I am very happy! And I promise to spread the good work of Lord Felix Morgan. If you are interested in joining the Illuminati New World Order today, contact Lord Felix Morgan today. This is your best chance to obtain the Illuminati membership you have always wanted. Contact Lord Felix Morgan via email: Illuminatiofficial565@gmail.com or WhatsApp +447353027456
HIRE Btc Hacker Web Recovery TO RECOVER YOUR LOST BITCOIN
If you’ve lost your Bitcoin to an online scam, hiring a professional recovery service can significantly improve your chances of getting your funds back. Btc Hacker Web Recovery specializes in Bitcoin recovery, helping victims reclaim their stolen assets. Here’s what you need to know:
Understanding the Recovery Process
The recovery process begins with contacting Btc Hacker Web Recovery. Their team will guide you through the steps necessary to initiate an investigation into your case. Understanding the process is key to managing your expectations.
Documenting Your Case
To facilitate recovery, it’s essential to document all relevant information regarding the scam. This includes transaction records, wallet addresses, and any communications with the scammer. Btc Hacker Web Recovery will help you gather this information to build a strong case.
Investigation and Tracking
Once you hire Btc Hacker Web Recovery, their experts will begin investigating your case. They use sophisticated tools to track the stolen Bitcoin, identifying the paths taken by the scammers. This tracing is crucial for successful recovery.
Freezing Stolen Assets
Quick action is vital in recovering stolen Bitcoin. Btc Hacker Web Recovery works directly with cryptocurrency exchanges to freeze any stolen assets, preventing the scammers from cashing out your funds. This collaboration is essential for a successful recovery.
Legal Support and Guidance
If necessary, Btc Hacker Web Recovery can provide legal support. They will guide you on reporting the scam to law enforcement and assist in filing any legal claims. Their expertise in crypto-related cases ensures you receive the best advice on how to proceed.
If you’ve lost Bitcoin to an online scam, don’t hesitate. Hire Btc Hacker Web Recovery to recover your lost assets and regain your financial security.
Email: btchacke@cyberservices.com
Telegram: @Btchackercyberservices
Post a Comment